Trellis-Oriented 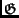$\mathfrak{G}$-codes

Table 6 lists the properties of some distance-8 lexicodes and trellis-oriented 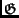$\mathfrak{G}$-codes. Over a binary field, lexicodes with odd minimum distance are simply punctured lexicodes with even minimum distance, so it is redundant to list their properties [5]. The minimum distance 4 lexicodes are all extended Hamming codes or shortenings thereof [5]. The minimum distance 6 and 8 codes we have computed also have optimal error-correction capability in the sense that each has the best known minimum distance for its length and dimension as compared to [2]. We can see that the trellis-oriented codes almost always have lower decoding complexity than the corresponding lexicodes; however, there are small pockets, where the trellis-oriented codes have higher state complexity and/or decoding complexity than lexicodes.