Relation Between Cosets

So far we have addressed the computation of various generating mappings. In this and subsequent sections we will complete our analysis by addressing the theoretical mechanism which supports the $\mathfrak{G}$-construction. Specifically, the $\mathfrak{G}$-construction establishes an important relationship between the coset leaders of the codes produced at successive iterations. This relationship allows us to efficiently compute the coset leaders of many $\ensuremath{{\mathfrak{G}}}$-codes (and hence their generator matrices) as well as to determine bounds on their code parameters. We describe this relationship by first associating a companion with each coset leader. Recall that a coset leader is a designated vector of minimum weight in a given coset.

Definition 2   The companion of a coset leader l, with respect to a vector v$\mbox{$ \inn $}$$\mathbb {F}$₂ⁿ, is the leader of the coset containing l + v. It is denoted $\kappa_{v}^{}$(l ), or $\kappa$(l ) in context.

We show that one iteration of the lexicographic construction produces a code whose coset leaders are either $\langle$a| u$\rangle$ or $\langle$$\bar{a}$|$\kappa$(u)$\rangle$ (depending on which has lower Hamming weight), for each vector a of appropriate size and coset leader u in the original code. Here $\bar{a}$refers to the complement of a.

Theorem 3   Consider an (n, k, d ) code $\ensuremath{{\mathbb{C}}}$ with a fixed set $\mathcal {S}$ of coset leaders, and the linear code $\ensuremath{{\mathbb{C}}}'$ spanned by $\ensuremath{{\mathbb{C}}}~\cup~\left\{ (1^{\Delta} \vert \lambda) \right\}$ for some $\lambda$$\mbox{$ \inn $}$$\mathbb {F}$₂ⁿ and $\Delta$$\mbox{$ \inn $}$$\mathbb {Z}$. Then the set $\mathcal {S}$^$\prime$ of coset leaders of $\ensuremath{{\mathbb{C}}}'$ can be obtained from $\mathcal {S}$ according to the following bijective correspondence:

$$\phi$$ : (a, l )$$\mbox{$\,\inn\,$}$${$$\langle$$0|$$\mathbb {F}$$₂^{$\Delta$ - 1}$$\rangle$$}×$$\mathcal {S}$$ $$\longmapsto$$ l'$$\mbox{$\,\inn\,$}$$$$\mathcal {S}$$^$\prime$

where l' is defined by the property

l' = $$\left\{\vphantom{ \begin{array}{ll} \langle a\vert l\rangle& \te... ...(\left\langle \bar{a}\vert\kappa_\lambda(l) \right\rangle). \end{array}}\right.$$$$\begin{array}{ll} \langle a\vert l\rangle& \text{if } \ensuremat... ...me{wt}} (\left\langle \bar{a}\vert\kappa_\lambda(l) \right\rangle). \end{array}$$

In other words, every coset of leader l in S, when paired with a vector a, produces a coset leader l' in S', and vice versa.

Proof: We introduce the following notation to simplify the proof:

$$\mbox{$\stackrel{\mathrm{\mbox{def}}}{=}$} \langle \rangle \mbox{$\stackrel{\mathrm{\mbox{def}}}{=}$} \left\langle\vphantom{ \bar{a}~\vert~\kappa_\lambda(l)}\right. \bar{a} \kappa_{\lambda}^{} \left.\vphantom{ \bar{a}~\vert~\kappa_\lambda(l)}\right\rangle$$ (9)

This proof then rests upon two observations. The first observation is that g(a, l ) and h(a, l ) are always in the same coset of the new code $\ensuremath{{\mathbb{C}}}'$. This is clear because:

$$\langle \left[\vphantom{ a+\bar{a} }\right. \bar{a} \left.\vphantom{ a+\bar{a} }\right] \left[\vphantom{ l+ \kappa(l) }\right. \kappa \left.\vphantom{ l+ \kappa(l) }\right] \rangle$$ g(a, l )  +  h(a, l )

$$\langle \Delta \left[\vphantom{ l+ (l+\lambda+c) }\right. \lambda \left.\vphantom{ l+ (l+\lambda+c) }\right] \rangle \mbox{$\,\inn\,$} \mathbb {C}$$

$$= \left\langle 1^\Delta \mid \lambda\right\rangle + \left\langle 0^\Delta \mid c\right\rangle$$

$$\mbox{$\,\inn\,$}\quad \ensuremath{{\mathbb{C}}}' .$$

Here $\Delta$ is the padding value, as presented in the statement of the theorem.

The second observation of this proof is that g(a, l ) and g(a', l') are generally not in the same coset of $\ensuremath{{\mathbb{C}}}'$. More specifically, these two vectors are in the same coset precisely when l and l' are in distinct cosets of  $\ensuremath{{\mathbb{C}}}$ and $\bar{a}$ $\not=$a'. To see this we analyze the two possibilities for the sum g(a, l )+ g(a', l'). In the first case, its leading bits are neither 0^$\Delta$ nor 1^$\Delta$. Alternatively, its leading bits are 0^$\Delta$ but its trailing bits are the sum of distinct coset leaders $l+ l' \not\inn \ensuremath{{\mathbb{C}}}$. Both possibilities preclude g(a, l )+ g(a', l') from being a codeword of $\ensuremath{{\mathbb{C}}}'$, proving the observation.

Based on the above two observations, g( ^. , ^. ) and h( ^. , ^. ) represent the same two-to-one correspondence between (vector, coset-leader) pairs (a, l ) and the cosets of $\ensuremath{{\mathbb{C}}}'$. In fact, for each a$\mbox{$ \inn $}$$\mathbb {F}$₂ⁿ and coset leader l of $\ensuremath{{\mathbb{C}}}$, the coset of g(a, l ) contains only the vectors:

$$\left\{\vphantom{ \begin{array}{l} \left\langle a \mid (l+c) \rig... ...e \\ \left\langle \bar{a} \mid (l+\lambda+c)\right\rangle \end{array}}\right.$$$$\begin{array}{l} \left\langle a \mid (l+c) \right\rangle \\ \left\langle \bar{a} \mid (l+\lambda+c)\right\rangle \end{array}$$

for any $c \mbox{$\,\inn\,$}\ensuremath{{\mathbb{C}}}$.

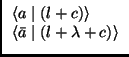
In addition, for any $c \mbox{$\,\inn\,$}\ensuremath{{\mathbb{C}}}$, g(a, l ) cannot have weight greater than the weight of $\left\langle\vphantom{ a\vert(l+c)}\right.$a|(l + c)$\left.\vphantom{ a\vert(l+c)}\right\rangle$, because l is a coset leader, and h(a, l ) cannot have weight greater than $\left\langle\vphantom{\bar{a}\vert(l+\lambda+c)}\right.$$\bar{a}$|(l + $\lambda$ + c)$\left.\vphantom{\bar{a}\vert(l+\lambda+c)}\right\rangle$. Therefore, all the vectors in the coset containing g(a, l ) will have weight not less than
[3] $\min \{\ensuremath{\operatorname{wt}}(\operatorname{g}(a,l)),\ensuremath{\operatorname{wt}}(\operatorname{h}(a,l))\}$, so that either g(a, l ) or h(a, l ) must be a coset leader in $\ensuremath{{\mathbb{C}}}'$. Since g(a, l ) and h(a, l ) are correspondences, $\mathcal {S}$^$\prime$ is the complete set of coset leaders of $\ensuremath{{\mathbb{C}}}'$.

width4pt depth2pt height6pt

Table 3 demonstrates the use of the $\phi$ correspondence of Theorem 3 to generate the coset leaders of the (7, 3, 4) binary lexicode $\ensuremath{{\mathcal{L}}_{4}^{3}}$ from the coset leaders of the (6, 2, 4) binary lexicode $\ensuremath{{\mathcal{L}}_{4}^{2}}$. In essence, the $\phi$ correspondence indicates that the coset leaders of a $\mathfrak{G}$-code are augmented permutations of the coset leaders of its predecessor in the $\mathfrak{G}$-construction. One such permutation produces the lexicodes, whereas other permutations produce the various other codes described in this paper.

Table 3: A list of coset leaders of the (7, 3, 4) lexicode. It is derived from the coset leaders of the (6, 2, 4) lexicode using Theorem 3 with $\lambda$ = 010010 and $\Delta$ = 1. Spaces between bits are used to highlight concatenations.

$$\bar{a} \kappa_{\lambda}^{} \mbox{$ \inn $} \mathcal{S'}$$ a | l

0 000000 1 010010 0 000000

0 000001 1 100000 0 000001

0 000010 1 010000 0 000010

0 000100 1 001000 0 000100

0 001000 1 000100 0 001000

0 010000 1 000010 0 010000

0 100000 1 000001 0 100000

0 001001 1 000000 1 000000