|
|
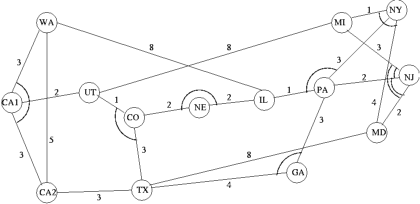
| Figure - Breaking all the cycles in a network using
turn-prohibition
|

Application of Network Calculus to General Topologies
Available in pdf(113k)
Network calculus is a general
paradigm for the provision of quality of
service (QoS) in communication networks.
The main principle of network calculus
is to show that if all the input flows to a network satisfy a certain set
of constraints, then so do all the flows within the network. The
formulation of the constraints is simple enough to allow the computation of bounds
on various performance measures, such as delay and queue length, at each
element of the network.
Network calculus is known to apply in
general only to feed-forward routing networks, i.e., networks where routes
do not create cycles of interdependent packet flows. In this project, we address the problem
of using network calculus in networks of
arbitrary topology. For this purpose, we introduce a novel algorithm,
called turn-prohibition (TP), that breaks all the cycles in a network
and, thus, prevents any
interdependence between flows. We prove that the TP-algorithm prohibits
the use of at most 1/3 of the total number turns in a
network, for any
network topology. Using analysis and simulation, we show that the
TP-algorithm significantly outperforms other approaches for breaking cycles, such as the
spanning tree and up/down routing algorithms, in terms of network
utilization and delay bounds. Our simulation results also show that the
network utilization achieved with the TP-algorithm is within a factor of
two of the maximum theoretical network utilization, for networks of up
to 50 nodes of degree four.
Thus, in many practical cases, the restriction of network calculus to
feed-forward routing networks may not represent a significant limitation.
Lab of Networking and Information Systems
Room 413 Photonics Building
8 St Mary's Street, Boston MA 02215
Web site created by Sachin Agarwal (ska@bu.edu)