Proof

It is well known (s.f.r. [15, p. 122]) for binomial distributions that, for 0 < b < ap:

$$\sum_{{i=0}}^{{b-1}} \choosei {\frac{{b(1-p)}}{{ap-b}}} \chooseb$$ (9)

Setting p = 1/2 in equation (2.12) gives us the following relation:

$$\chooseb \left(\vphantom{ \frac{a}{b} -2 }\right. {\frac{{a}}{{b}}} \left.\vphantom{ \frac{a}{b} -2 }\right) \sum_{{i=0}}^{{b-1}} \chooseb$$

Since we have assumed that a > 3b, we have that ${\frac{{a}}{{b}}}$ - 2 > 1 and the lemma is proved.

width4pt depth2pt height6pt

We proceed to the proof of Theorem 2.7.

Proof of Theorem 2.7.  Following convention, we let $t = \ensuremath {\left\lfloor (d-1)/2 \right\rfloor}$ denote the number of errors that the codes of a G-family can correct. It is well-known that each vector in $\mathbb {F}$₂^n_m-1 of weight $\leq$ t must be a unique coset leader for G _m-1. Moreover, using our assumption about n₀ (which also holds for n_m, since n_m $\geq$ n₀), Lemma 2.8 implies that

$$\choose {t} \sum_{{i=0}}^{{t-1}} \choosei$$ (9)

The left-hand side of (2.13) is the number of vectors of weight t, while the right-hand side is the number of vectors of weight < t. Thus, by the pigeon-hole principle, there must be at least one coset leader $l\mbox{$\,\inn\,$}\ensuremath{ {\emph G}_{\,m-1}}$ of weight t whose companion $\kappa$(l ) has weight at least t. Since $\Delta_{m}^{}$ $\geq$ d - $\rho_{{m-1}}^{}$ for any G-code, we may choose $a=0^{\ensuremath {\left\lfloor {\Delta_m}/2 \right\rfloor}}1^{\ensuremath {\left\lceil {\Delta_m}/2 \right\rceil}}$ to get:

$$\rho_{m}^{} \geq \left\{\vphantom{wt(\langle a \mid l\rangle), \ensuremath{\operatorname{wt}}\left( \langle \bar{a} \mid \kappa_v(l) \rangle \right)}\right. \langle \rangle \left(\vphantom{ \langle \bar{a} \mid \kappa_v(l) \rangle }\right. \langle \bar{{a}} \kappa_{v}^{} \rangle \left.\vphantom{ \langle \bar{a} \mid \kappa_v(l) \rangle }\right) \left.\vphantom{wt(\langle a \mid l\rangle), \ensuremath{\operatorname{wt}}\left( \langle \bar{a} \mid \kappa_v(l) \rangle \right)}\right\}$$

$$= \ensuremath {\left\lfloor \frac{{\Delta_m}}{2} \right\rfloor}+ t$$

$$\geq \ensuremath {\left\lfloor \frac{d-\rho_{m-1}}{2} \right\rfloor}+ \ensuremath {\left\lfloor \frac{d-1}{2} \right\rfloor}$$

width4pt depth2pt height6pt

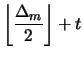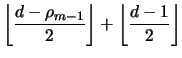The result in Theorem 2.7 also applies to all G-families trivially seeded with the code $\mathbb {S}$_d.

Lemma 2..9   For any trivially seeded G-family of codes,

$$\rho_m \ \geq \ \ensuremath {\left\lfloor \frac{d-1}{2} \rig... ...\ensuremath {\left\lfloor \frac{d-\rho_{m-1}}{2} \right\rfloor}$$

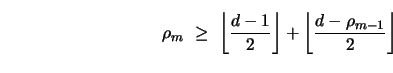
If a G-family is trivially seeded, then, necessarily, n₀ = d and $\rho_0 = \ensuremath {\left\lfloor \frac{d}{2} \right\rfloor}$.Thus,

$$n_1 = n_0 + (d - \rho_0) = d + \ensuremath {\left\lceil \fra... ...l}\geq 3 \ensuremath {\left\lfloor \frac{d-1}{2} \right\rfloor}$$

so that Theorem 2.7 applies to the remaining codes in the family.

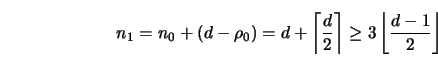
We now turn our attention to generating mappings which produce codes whose information rate is locally maximized. More specifically, for any code $\ensuremath{\mathbb{C}}$ with covering radius $\rho_{{\ensuremath{\mathbb{C}}}}^{}$, we will consider only generating mappings f with the property that the Hamming distance from $\ensuremath{\mathbb{C}}$ to $f(\ensuremath{\mathbb{C}})$ is exactly $\rho_{{\ensuremath{\mathbb{C}}}}^{}$. We will call such mappings minimal generating mappings, and the corresponding family of codes minimal G-codes, because they locally minimize length (and hence locally maximize information rate) for a given dimension and minimum-distance.

As an example, the generating mappings for the traditional lexicodes and the trellis-oriented lexicodes are both minimal. We may now easily strengthen Lemma 2.6 by observing in its proof that $\Delta_{m}^{}$ = d - $\rho_{{m-1}}^{}$ for minimal G-codes.

Corollary 2..10   For any minimal G-family of codes,

$$\rho_m \ \leq \ \ensuremath {\left\lfloor \frac{d+\rho_{m-1}}{2} \right\rfloor}$$

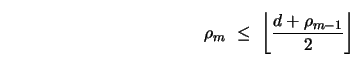
The covering radius bounds we have developed for G-codes translates naturally to length bounds as well.