Next: Proof of the main Up: The minimum distance of Previous: The minimum distance of Contents
The following lemma will be the basis for the induction in our proof of Theorem 3.6.
Proof.
Let T(H) be the Tanner graph of H.
We now construct another graph ![]() , called the row-graph
of H, whose vertex set
y1, y2,..., yr-s corresponds to
the rows of H.
The edge set of
, called the row-graph
of H, whose vertex set
y1, y2,..., yr-s corresponds to
the rows of H.
The edge set of ![]() is derived from the columns of H
of weight
is derived from the columns of H
of weight ![]() 2, so that a column of weight w in H
contributes w - 1 edges to
2, so that a column of weight w in H
contributes w - 1 edges to ![]() .
An example illustrating the construction of the row-graph
.
An example illustrating the construction of the row-graph ![]() for
a
6×8 cycle-free matrix is depicted in Figure 3.3.
for
a
6×8 cycle-free matrix is depicted in Figure 3.3.
Specifically, there is
an edge between yi and yj in ![]() iff i < j and
there exists a column
(a1, a2,..., ar-s)t in H,
such that
ai = aj = 1 while
ai+1 = ai+2 = ... = aj-1 = 0.
Notice that each such edge (yi, yj) in
iff i < j and
there exists a column
(a1, a2,..., ar-s)t in H,
such that
ai = aj = 1 while
ai+1 = ai+2 = ... = aj-1 = 0.
Notice that each such edge (yi, yj) in ![]() corresponds to
a path of length two in T(H): namely
corresponds to
a path of length two in T(H): namely
![]() (yi, xp),(xp, yj)
(yi, xp),(xp, yj)![]() ,
where p denotes the position at which the column
(a1, a2,..., ar-s)t is to be found in H.
It follows that if there is a cycle in
,
where p denotes the position at which the column
(a1, a2,..., ar-s)t is to be found in H.
It follows that if there is a cycle in ![]() , then there
is a cycle in T(H). Since T(H) is cycle-free, then
so is
, then there
is a cycle in T(H). Since T(H) is cycle-free, then
so is ![]() . As such,
. As such, ![]() necessarily contains at least two vertices
of degree
necessarily contains at least two vertices
of degree ![]() 1, in view of (3.2).
Let y* be one such vertex in
1, in view of (3.2).
Let y* be one such vertex in ![]() , and let
a* = (a1, a2,..., an-s) be the corresponding
row of H. If
, and let
a* = (a1, a2,..., an-s) be the corresponding
row of H. If
![]() , then (
, then (![]() ) is true.
If
) is true.
If
![]() and
deg y* = 0, then
(
and
deg y* = 0, then
(![]() ) is true.
If
) is true.
If
![]() and
deg y* = 1, then (
and
deg y* = 1, then (![]() ) is true.
Finally, if
) is true.
Finally, if
![]() , then
(
, then
(![]() ) is true,
regardless of whether
deg y* = 0 or
deg y* = 1.
) is true,
regardless of whether
deg y* = 0 or
deg y* = 1.
width4pt depth2pt height6pt
Let
![]() be an (n, k, d ) cycle-free binary linear code, and let
H be an
r×n cycle-free parity-check matrix for
be an (n, k, d ) cycle-free binary linear code, and let
H be an
r×n cycle-free parity-check matrix for
![]() ,
where r = n - k. We say that H is in s-canonical form
if this matrix has the following structure:
,
where r = n - k. We say that H is in s-canonical form
if this matrix has the following structure:
Lemma 3.7 trivially generalizes to matrices in s-canonical form.
Proof.
Evidently T(A) is
a subgraph of T(H), obtained by retaining only the first
n - s symbol vertices
x1, x2,..., xn-s, the first
r - s check vertices
y1, y2,..., yr-s, and all the
edges between these vertices. Since T(H) is
cycle-free by assumption, so is T(A). Thus, Lemma 3.7
applies to complete the proof.
width4pt depth2pt height6pt
We will say that an
r×n matrix H is in reduced canonical form,
if
H = A|sB and either s = r or all the rows of A have
weight ![]() 3. It is a non-trivial fact that every cycle-free parity-check matrix can be put into such a form.
3. It is a non-trivial fact that every cycle-free parity-check matrix can be put into such a form.
Proof.
Let H be an arbitrary cycle-free parity-check matrix for
![]() .
We first put H in s-canonical form, for the highest possible s,
by means of row and column permutations. This is achieved by
considering all the rows of H of weight one, for which
the nonzero entry * is contained in a column of weight one,
and all the rows of H of weight two such that at least one of the two *'s is contained in a column of weight
one. Under an appropriate column permutation, these rows of H
will form the submatrix
[B | Is] in (3.7).
If there are no such rows, then s = 0 and H = A.
Since row and column permutations preserve the cycle-free
property of H, this procedure produces a cycle-free
parity-check matrix
H' = A|sB for
.
We first put H in s-canonical form, for the highest possible s,
by means of row and column permutations. This is achieved by
considering all the rows of H of weight one, for which
the nonzero entry * is contained in a column of weight one,
and all the rows of H of weight two such that at least one of the two *'s is contained in a column of weight
one. Under an appropriate column permutation, these rows of H
will form the submatrix
[B | Is] in (3.7).
If there are no such rows, then s = 0 and H = A.
Since row and column permutations preserve the cycle-free
property of H, this procedure produces a cycle-free
parity-check matrix
H' = A|sB for
![]() , which
is in canonical form, although not necessarily reduced.
, which
is in canonical form, although not necessarily reduced.
Since
H' = A|sB is full-rank by assumption, all the rows of A
have weight ![]() 1. The key observation is that certain elementary
operations on the rows of H' allow us to eliminate rows of
weight one and two in A, while still preserving the cycle-free
property.
1. The key observation is that certain elementary
operations on the rows of H' allow us to eliminate rows of
weight one and two in A, while still preserving the cycle-free
property.
Indeed, suppose that A has a row
(a1, a2,..., ar-s) of weight one,
with a single * in position i. Then we can add this row to all the
rows of H' that are nonzero at position i. This procedure is equivalent
to deleting all but one of the edges incident at the symbol vertex xi
in T(H'), which certainly does not create new cycles.
Following this procedure, the single * in
(a1, a2,..., ar-s)
is contained in a column of weight one. Hence we can transform the
resulting cycle-free parity-check matrix for
![]() into the form
A'|s+1B', by means of row and column permutations, thereby
eliminating the row of weight one in A.
into the form
A'|s+1B', by means of row and column permutations, thereby
eliminating the row of weight one in A.
Now suppose that A has a row
(a1, a2,..., ar-s) of weight two,
with the two *'s in positions i and j, and let y* be the corresponding
check vertex in T(H'). We again add this row to all the rows of H' that
are nonzero at position i. Let
(b1, b2,..., bn) be such a row,
and let y' denote the corresponding check vertex of T(H'). If
bj = bi = *, then T(H') contains the
cycle
![]() (xi, y*),(y*, xj),(xj, y'),(y', xi)
(xi, y*),(y*, xj),(xj, y'),(y', xi)![]() .
Since T(H') is cycle-free, we conclude that bi = * while bj = 0.
Hence, adding row
(a1, a2,..., an) to
(b1, b2,..., bn)
corresponds to deleting the edge (y', xi) in T(H') while
introducing a new edge (y', xj), as illustrated in Figure 3.4.
.
Since T(H') is cycle-free, we conclude that bi = * while bj = 0.
Hence, adding row
(a1, a2,..., an) to
(b1, b2,..., bn)
corresponds to deleting the edge (y', xi) in T(H') while
introducing a new edge (y', xj), as illustrated in Figure 3.4.
However, this new edge cannot
close a cycle, since T(H') is cycle-free and a path from y'
to xj already exists in T(H'): indeed
![]() (y', xi),(xi, y*),(y*, xj)
(y', xi),(xi, y*),(y*, xj)![]() is such a path.
Following all these elementary row operations, the * at position i
in
(a1, a2,..., an) is contained in a column of weight one. Thus
we can again transform the resulting cycle-free parity-check matrix for
is such a path.
Following all these elementary row operations, the * at position i
in
(a1, a2,..., an) is contained in a column of weight one. Thus
we can again transform the resulting cycle-free parity-check matrix for
![]() into the form
A'|s+1B',
thereby eliminating the row of weight two in A.
into the form
A'|s+1B',
thereby eliminating the row of weight two in A.
We iteratively repeat the process described in the foregoing two paragraphs,
until either s = r or all the rows of A have weight ![]() 3.
This procedure produces a cycle-free parity-check matrix for
3.
This procedure produces a cycle-free parity-check matrix for
![]() that
is in reduced canonical form.
that
is in reduced canonical form.
width4pt depth2pt height6pt
If the reduced canonical form in Lemma 3.9 is achieved in the extreme case s = r, then it is easy to prove the claim of Theorem 3.6.
Proof.
If B contains a column of weight w, then clearly d![]() w + 1.
Since B is an
r×k matrix, there will always be at least
one column with maximum weight
w + 1.
Since B is an
r×k matrix, there will always be at least
one column with maximum weight
![]() , so that
, so that
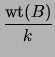 + 1.
+ 1.
http://people.bu.edu/trachten