|
|
Dim- |
Standard |
Trellis- |
Standard |
Trellis- |
Standard |
Trellis- |
|
ension | |
oriented | |
oriented | |
oriented
|
| Length | Length | States | States |
2| E| - | V| + 1 |
2| E| - | V| + 1 |
|
1 | 8 | 1 | 17 |
| 2 | 12 | 2 | 35 |
| 3 | 14 | 3 | 71 |
| 4 | 15 | 4 | 143 |
| 5 | 16 | 4 | 195 |
| 6 | 18 | 5 | 341 |
| 7 | 19 | 6 | 647 |
| 8 | 20 | 6 | 779 |
| 9 | 21 | 7 | 1,547 |
| 10 | 22 | 8 | 2,395 |
| 11 | 23 | 9 | 4,219 |
| 12 | 24 | 9 | 4,475 |
| 13 | 28 | 9 | 4,529 |
| 14 | 30 | 9 | 4,777 |
| 15 | 31 | 9 | 5,463 |
| 16 | 32 | 9 | 5,515 |
| 17 | 34 | 9 | 7,645 | 5,693 |
| 18 | 35 | 9 | 12,671 | 6,143 |
| 19 | 36 | 9 | 12,803 | 6,275 |
| 20 | 37 | 10 | 9 | 24,267 | 7,691 |
| 21 | 38 | 10 | 9 | 25,115 | 8,539 |
| 22 | 39 | 10 | 9 | 26,939 | 10,363 |
| 23 | 40 | 10 | 9 | 27,195 | 10,619 |
| 24 | 42 | 10 | 31,805 | 17,853 |
| 25 | 43 | 11 | 41,791 | 33,087 |
| 26 | 44 | 11 | 41,987 | 33,283 |
| 27 | 45 | 12 | 65,227 |
| 28 | 46 | 12 | 67,163 |
| 29 | 47 | 12 | 72,571 | 78,203 |
| 30 | 48 | 12 | 72,827 | 78,459 |
| 31 | 49 | 50 | 13 | 12 | 135,611 | 80,317 |
| 32 | 50 | 51 | 13 | 12 | 169,019 | 87,103 |
| 33 | 51 | 52 | 13 | 12 | 248,123 | 88,643 |
| 34 | 52 | 53 | 13 | 248,507 | 137,547 |
| 35 | 53 | 54 | 14 | 13 | 427,579 | 138,331 |
| 36 | 54 | 55 | 14 | 13 | 431,419 | 142,203 |
| 37 | 55 | 56 | 14 | 13 | 442,171 | 142,459 |
| 38 | 56 | 57 | 14 | 442,555 | 274,875 |
| 39 | 58 | 14 | 487,997 | 308,283 |
| 40 | 59 | 14 | 628,031 | 457,019 |
| 41 | 60 | 14 | 628,227 | 460,091 |
| 42 | 62 | 14 | 629,197 | 460,861 |
| 43 | 63 | 14 | 631,903 | 464,703 |
| 44 | 64 | 14 | 632,035 | 464,899 |
| 45 | 65 | 15 | 14 | 1,263,819 | 581,835 |
| 46 | 66 | 15 | 1,287,195 | 1,053,275 |
|
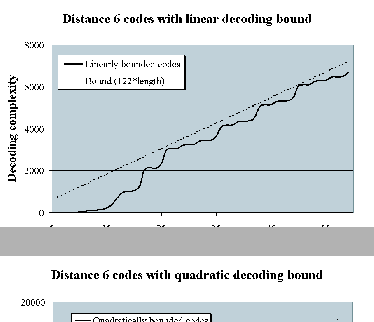
![]() -codes.
Specifically, it shows the decoding
complexity achieved under linear and quadratic decoding bounds. The
degradation in code length compared to the standard lexicodes is modest
for these examples.
-codes.
Specifically, it shows the decoding
complexity achieved under linear and quadratic decoding bounds. The
degradation in code length compared to the standard lexicodes is modest
for these examples.