Lexicodes

As mentioned in the previous section, the mapping $\ensuremath{f_{\mbox{\small lexi}}}$ generates the lexicodes. The computation of $\ensuremath{f_{\mbox{\small lexi}}}$ is handled by a simple greedy algorithm, presented as Method 1, which operates in linear time (in its inputs), subject to appropriate knowledge of the input code. The speed with which we can compute $\ensuremath{f_{\mbox{\small lexi}}}$ permits efficient generation of lexicodes, as we shall see later in Section 5.

In order to compute $\ensuremath{f_{\mbox{\small lexi}}}$ we will first transform the generator matrix of the code into a minimal span generator matrix (MSGM) form, in which the sum of the spans of the generators is minimized. Adapting the notation in [11], the span of a binary n-vector x = (x₁, x₂, x₃,..., x_n) is $\ensuremath{\operatorname{R}}(x)-\ensuremath{\operatorname{L}}(x)$, where $\ensuremath{\operatorname{R}}(\cdot)$ and $\ensuremath{\operatorname{L}}(\cdot)$ are the rightmost (i.e., largest) and leftmost (i.e., smallest) index i, respectively, such that x_i $\not=$ 0. Thus, the span of the vector x = (0001001100) is $\ensuremath{\operatorname{R}}(x)-\ensuremath{\operatorname{L}}(x)=8-4=4$. We can efficiently transform any matrix into MSGM form using the greedy algorithm in [11]. We note that two vectors of an MSGM cannot have their leftmost or their rightmost index in common, or else they may be added to produce a generator matrix with shorter span.

Given an MSGM for a code and a set of coset representatives $\mathcal{V}$, Method 1 computes the lexicographically earliest vector among the cosets represented in $\mathcal{V}$.

Method 1   Consider a set of vectors $\mathcal{V}$ representing cosets of a code $\mathbb {C}$ whose length is n. Let G be an MSGM for  $\ensuremath{{\mathbb{C}}}$ whose generators are in lexicographically increasing order (i.e., $G_1 \ensuremath{<_{\mbox{lexi}}}G_2 \ensuremath{<_{\mbox{lexi}}}G_3 \ldots \ensuremath{<_{\mbox{lexi}}}G_n$). The following greedy method computes the lexicographically earliest vector among the represented cosets in O(n| V|) time and O(n) space.

1. for each
v = (v1, v2, v3,..., v|$\mathcal {V}$|)$\mbox{$ \inn $}$$\mathcal{V}$ do


2. 		 		fori from n down to 1


3. 		 		 		if 
$v_{\ensuremath{\operatorname{L}}(G_i)}$ is a 1 then


4. 		 		 		 		
v $\leftarrow$ v + Gi


5. 		 		store the modified v


6. 		 among all stored v, return the lexicographically earliest

This method looks for the generators whose left-most 1-bit corresponds to 1-bits in vectors v$\mbox{$ \inn $}$V. Figure 2 demonstrates this method with the set $\mathcal{V}$ = {1010000} on the (7, 4, 3) code described in Table 1. For this case, the vector 0001011 is the lexicographically earliest vector in the same coset as 1110000. Note that the ordering of the generators in the MSGM is significant and that different orderings might not yield the lexicographically earliest vector. For example, if generators G₂ and G₃ are switched, then Method 1 yields 0010010, which is not the lexicographically earliest vector desired.

Figure: Method 1 applied to the code in Table 1 with initial condition $\mathcal{V}$ = {1110000}. The various values taken on by v during the computation are shown on the right-hand region.

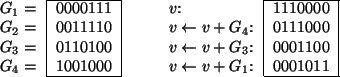We will now prove the correctness of Method 1. In our applications, $\mathcal{V}$ will typically be the set of leaders of cosets with maximum distance from $\ensuremath{{\mathbb{C}}}$. These coset leaders are defined to be the minimum-weight vectors in their corresponding cosets, so that Method 1 computes precisely $\ensuremath{f_{\mbox{\small lexi}}}(\ensuremath{{\mathbb{C}}})$.

Proof of Method 1: We first show correctness of the method by proving that, for each v$\mbox{$ \inn $}$$\mathcal{V}$, lines 2-5 compute the lexicographically earliest vector in the same coset as v. This way, line 6 in the method will return the lexicographically earliest vector among all the cosets represented.

We know from [11, Thm 6.11 and Lemma 6.7] that the rows of G have the predictable support property:

$$\left(\vphantom{\sum_{j \mbox{$\,\inn\,$}J} G_j }\right. \sum_{j \mbox{$\,\inn\,$}J}^{} \left.\vphantom{\sum_{j \mbox{$\,\inn\,$}J} G_j }\right) \bigcup_{j \mbox{$\,\inn\,$}J}^{}$$ (3)

for every subset J $\subseteq$ {1, 2, 3,..., n}.

Now suppose that $\ensuremath{v_{\mathrm{best}}}$ is the lexicographically earliest vector in the same coset as v, but that instead $\ensuremath{v_{\mathrm{stored}}}$ is the vector stored on line 5 of the method. Our goal will be to show that the difference between these two vectors, denoted $\ensuremath{v_{\mathrm{diff}}}$, is in fact 0.

Clearly v, $\ensuremath{v_{\mathrm{best}}}$, and $\ensuremath{v_{\mathrm{stored}}}$ are necessarily in the same coset of $\ensuremath{{\mathbb{C}}}$. Moreover, since v and $\ensuremath{v_{\mathrm{stored}}}$ are in the same coset, $\ensuremath{v_{\mathrm{diff}}}$ must be a codeword of $\ensuremath{{\mathbb{C}}}$ so that we can write (for an appropriate set $J_{\ensuremath{{\mathrm{diff}}}}$):

$$\sum_{j \mbox{$\,\inn\,$}J_{\ensuremath{{\mathrm{diff}}}}}^{}$$ (4)

Then, applying the predictable span property of G,

$$\bigcup_{j \mbox{$\,\inn\,$}J_{\ensuremath{{\mathrm{diff}}}}}^{}$$ (5)

Assume (for sake of contradiction) that $L(\ensuremath{v_{\mathrm{diff}}}) = k$, meaning that the left-most 1 bit of $\ensuremath{v_{\mathrm{diff}}}$ occurs at the k-th index. This implies that, starting from the left-most bit, $\ensuremath{v_{\mathrm{best}}}$ and $\ensuremath{v_{\mathrm{stored}}}$ are identical until the k-th index, on which they differ. Since, by definition, $\ensuremath{v_{\mathrm{best}}}$ comes lexicographically before $\ensuremath{v_{\mathrm{stored}}}$, it must be that $\ensuremath{v_{\mathrm{best}}}$ has a 0 and $\ensuremath{v_{\mathrm{stored}}}$ a 1 at the k-th index. Then (6) implies that there must be some generator G_j whose left-index is k; however, the lexicographic ordering of the generators insures that G_j would have eliminated any 1 at index k in $\ensuremath{v_{\mathrm{stored}}}$, providing a contradiction. Thus, the left-index of $\ensuremath{v_{\mathrm{diff}}}$ could not possibly be at location k, for any k, so that $\ensuremath{v_{\mathrm{diff}}}$ must be 0 and correctness of the method is proved. The time bound follows straightforwardly, and the space bound follows from noting that only the lexicographically earliest vector v needs to be stored in line 5 of the method.

width4pt depth2pt height6pt

Method 1 provides a fast way of computing the lexicographic generating mapping. Appendix .1 gives computed parameters for many lexicodes that were thus computed. This list is more exhaustive than what is currently available in the literature [3,5].