The lexicographic construction

A q-ary, length n, minimum distance d lexicode is traditionally defined constructively based on a lexicographic (i.e. dictionary) ordering of vectors in which, for example, 01111 comes before 10000. The construction starts with the set $\mathcal {S}$ = {$\bf0\}$ and greedily adds, until exhaustion, the lexicographically earliest vector (in the vector space $\mathbb {F}$_qⁿ) whose Hamming distance from $\mathcal {S}$ is at least d.

For example, the codewords of the binary lexicode (i.e. q = 2) of length n = 3 and minimum distance d = 2 are marked by a $\bullet$ in Figure  and would be computed left-to-right across the figure.

Figure 2.1: A simple n = 3, d = 2 binary lexicode.

This greedy construction always generates a linear code [9,14]. Thus, we may completely describe a dimension k lexicode by finding its k generators using what we call the lexicographic construction. This construction starts with the zero code $\ensuremath{\mathcal{L}_{0}^{d}}=\mathbf{0}$ and greedily adds the lexicographically earliest generator of distance d from the code; k such iterations form the dimension k code $\ensuremath{\mathcal{L}_{k}^{d}}$. Figure 2.2 demonstrates this construction for d = 3, resulting in a (7, 4, 3) binary code.

Figure 2.2: Generator matrix for the dimension 4, minimum distance 3 binary code $\mathcal {L}$₄³. The generator padding for each iteration is marked in bold.

We may understand the lexicographic construction more analytically by making use of the covering radius of each intermediate code $\ensuremath{\mathcal{L}_{i}^{d}}$ in the iteration. The covering radius of a length n code is the smallest integer $\rho$ with the property that Hamming balls of radius $\rho$ centered at codewords of the code will cover every vector of $\mathbb {F}$_qⁿ. In other words, $\rho$ is the maximum distance of a vector in $\mathbb {F}$_qⁿ from the code. As an example, one can readily see that the binary lexicode in Figure 2.1 has a covering radius of 1 because every vector in $\mathbb {F}$₂³ is at most of Hamming distance 1 from a code vector.

An iteration of the lexicographic construction on an intermediate code $\ensuremath{\mathbb{C}}$ whose covering radius is $\rho$ and minimum distance is d can thus be understood as the addition of a generator vector:

$$\langle 1^{d-\rho}\; \vert\; \ensuremath{f_{\mbox{\small lexi}}}(C) \rangle$$

where 1^d-$\rho$, known as the generator padding, has the usual meaning of (d - $\rho$) successive 1's, and the function $\ensuremath{f_{\mbox{\small lexi}}}(\ensuremath{\mathbb{C}})$ returns the lexicographically earliest vector of distance $\rho$ from $\ensuremath{\mathbb{C}}$. As is customary, we use $\langle$ ^. | ^. $\rangle$ to denote concatenation.

It is not surprising that the non-trivial^2.1linear codes generated by the lexicographic construction described above are precisely the lexicodes.

Theorem 2..1   Over a finite field $\mathbb {F}$_q, a non-trivial (n, k, d ) code $\mathbb {C}$ is a lexicode if and only if it is produced by the lexicographic construction, namely $\mathbb{C}=\ensuremath{\mathcal{L}_{k}^{d}}$.

Proof.  We first prove that $\mathcal {L}$_k^d is always a lexicode, by induction on k for an arbitrary, fixed d. For the base case it is clear that $\ensuremath{\mathcal{L}_{1}^{d}}= \left\{0^d,1^d\right\}$ is a (d, 1, d ) lexicode. Now assume as an inductive hypothesis that $\mathcal {L}$_k^d is the same as the (n, k, d ) lexicode  $\ensuremath{\mathbb{C}}_k$. From the definition of the lexicographic construction, $\mathcal {L}$_k+1^d has parameters (n + $\rho$, k + 1, d ), where $\rho$ is the covering radius of $\mathcal {L}$_k^d. Consider the (n + $\rho$, k', d ) lexicode $\ensuremath{\mathbb{C}}_{k'}$ constructed by repeatedly choosing the appropriate lexicographically-earliest vectors in $\mathbb {F}$_q^n+$\rho$. Clearly, we generate $\ensuremath{\mathbb{C}}_k$ in the process of this construction, so that $\ensuremath{\mathbb{C}}_k \subseteq \ensuremath{\mathbb{C}}_{k'}$ and, by the inductive hypothesis, $\ensuremath{\mathcal{L}_{k}^{d}}\subseteq \ensuremath{\mathbb{C}}_{k'}$. Moreover, the vector

$$v = \left\langle 1^{d-\rho} \:\vert\: \ensuremath{f_{\mbox{\small lexi}}}( \ensuremath{\mathbb{C}}_k )\right\rangle$$

is the lexicographically earliest vector of distance $\rho$ from $\ensuremath{\mathcal{L}_{k}^{d}}$. Thus, it must be the case that v$\mbox{$\,\inn\,$}$C_k' and, since C_k' is linear, $\ensuremath{\mathcal{L}_{k+1}^{d}}\subseteq \ensuremath{\mathbb{C}}_{k'}$.

Figure 2.3: The structure of the (k+1)-th lexicode $\mathcal {L}$_k+1^d. There are d - $\rho$ ones on the left-hand side. Since the covering radius of $\mathcal {L}$_k^d is $\rho$, any n bits (i.e. the vector w) must be at distance $\leq$ $\rho$ from the n rightmost bits of $\mathcal {L}$_k+1^d.

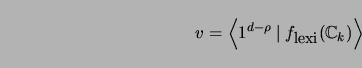
In addition, any vector v$\mbox{$\,\inn\,$}$$\mathbb {F}$_q^n+$\rho$ that is in $\ensuremath{\mathbb{C}}_{k'}$ but not in $\mathcal {L}$_k+1^d would necessarily have its n right-most bits at distance $\leq$ $\rho$ from $\mathcal {L}$_k+1^d, and its other bits at distance $\leq \ensuremath {\left\lceil (d-\rho)/2 \right\rceil}$ from $\mathcal {L}$_k+1^d, as we can see in Figure 2.3. Noting that our non-triviality assumption implies that $\rho$ < d, we may now use the triangle inequality to see that the distance from v to $\mathcal {L}$_k+1^d (and consequently also $\ensuremath{\mathbb{C}}_{k'}$) must be at most

$$\rho + \ensuremath {\left\lceil (d-\rho)/2 \right\rceil}\ = \ \ensuremath {\left\lceil (d+\rho)/2 \right\rceil}\ < \ d.$$

This contradicts our constructive definition of  $\ensuremath{\mathbb{C}}_{k'}$, so it must be that $\ensuremath{\mathcal{L}_{k+1}^{d}}=\ensuremath{\mathbb{C}}_{k'}$.

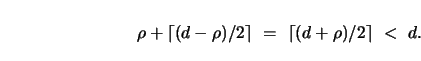
For the converse assertion of the theorem, we need to show that a non-trivial (n, k, d ) lexicode $\ensuremath{\mathbb{C}}$ can be constructed by the lexicographic construction. The code $\mathcal {L}$_k^d produced by k iterations of the minimum-distance d lexicographic construction is clearly a lexicode, from the first part of the proof. Since all distance d lexicodes are ordered by inclusion, as we saw in the first part of this proof, we may conclude that either $\ensuremath{\mathbb{C}}\subseteq \ensuremath{\mathcal{L}_{k}^{d}}$ or $\ensuremath{\mathcal{L}_{k}^{d}}\subseteq \ensuremath{\mathbb{C}}$. However $\ensuremath{\mathcal{L}_{k}^{d}}$ and $\ensuremath{\mathbb{C}}$ are both non-trivial dimension k codes, so it follows that they must be equal.

width4pt depth2pt height6pt

Theorem 2.1 allows us to bypass the codeword-by-codeword lexicode construction, and instead directly compute the generator matrix of a desired lexicode.