Code improvement

The G-construction also enables us to refine the trellis complexity of a given code. Theorem 2.3 assures us that $\ensuremath{f_{\mbox{\small trelli}}}(\cdot)$ is a locally optimal method of extending an arbitrary subcode if we seek to maximize information rate and minimize decoding complexity. Thus, we have a simple, greedy method in which we may attempt to improve a given code $\mathbb {C}$.

Specifically, we may arbitrarily delete a generator of $\mathbb {C}$ and replace it with a trellis-oriented generator. Because of Theorem 2.3 we know that the resulting code will have trellis complexity and code parameters (e.g. length, minimum distance) no worse than the original code.^2.2

In fact, this method may be applied to several generators: shorten $\mathbb {C}$ by deleting k generators; replace the generators with k trellis-oriented generators. This allows us to create an amalgam of the original code and a trellis-oriented code. Though the resulting code is not guaranteed to match the decoding performance of our original code, it often performs much better as we see in the following example.

Example 2..14   Consider the length 31, dimension 16, triple error-correcting BCH code generated by the polynomial

g(x) = 1 + x + x² + x³ + x⁵ + x⁷ + x⁸ + x⁹ + x¹⁰ + x¹¹ + x¹⁵.

It requires 2¹⁵ = 32, 768 trellis states and 262, 139 steps for Viterbi decoding. Figure 2.10 shows the dramatic improvement of this code as more generator vectors are replaced with trellis-oriented generators.

Figure 2.10: Improving a (31, 16, 7) BCH code by replacing k of its generators with trellis-oriented generators. The trellis state complexity and Viterbi decoding complexity of the intermediate (31, 16, 7) codes is noted, as is the time (in minutes) needed to compute them on a Sun Ultra-Sparc 1 workstation.

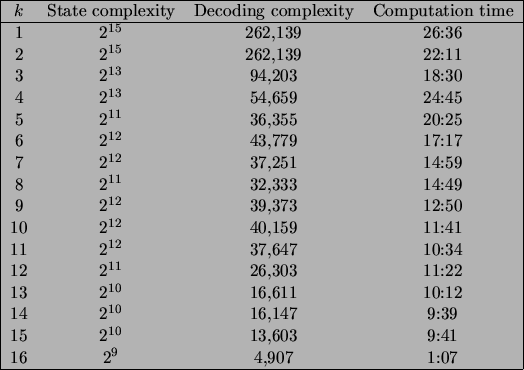We note that both the state and decoding complexities generally decrease as k increases. Moreover, the computation time also generally decreases because of the decreasing size of the seed code.