It is obvious from Theorem 3.6 that Tanner graphs without cycles cannot
support asymptotically good codes. Starting with Theorem 3.6, it is not
difficult to show that the same is true for Tanner graphs with cycles,
unless the number of cycles increases exponentially with the length
of the code as
n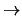
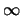 . To see this, suppose the the cycle rank
of a Tanner graph T = (V, E) representing an (n, k, d ) code
. To see this, suppose the the cycle rank
of a Tanner graph T = (V, E) representing an (n, k, d ) code
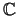 is
c = | E| - | V| +
is
c = | E| - | V| + 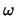 (T). This means that T contains 2c
cycles and unions of disjoint cycles (cf. [48, p.137]).
Now let xi be a symbol vertex that lies on a cycle in T.
Then removing xi and all the edges incident on xi from T
produces a graph whose cycle rank is strictly less than c.
This procedure is equivalent to shortening
(T). This means that T contains 2c
cycles and unions of disjoint cycles (cf. [48, p.137]).
Now let xi be a symbol vertex that lies on a cycle in T.
Then removing xi and all the edges incident on xi from T
produces a graph whose cycle rank is strictly less than c.
This procedure is equivalent to shortening
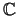 at the i-th
position to obtain an
(n', k', d') code
at the i-th
position to obtain an
(n', k', d') code
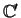 with n' = n - 1,
k'
with n' = n - 1,
k'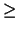 k - 1, and d'
k - 1, and d'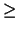 d.
Since the cycle rank strictly decreases each time we cut a cycle
in T in this way, after repeating this procedure t
d.
Since the cycle rank strictly decreases each time we cut a cycle
in T in this way, after repeating this procedure t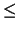 c times
we obtain a cycle-free code
c times
we obtain a cycle-free code
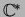 . Clearly
. Clearly
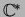 is an
(n*, k*, d*)
code with n* = n - t,
k*
is an
(n*, k*, d*)
code with n* = n - t,
k*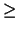 k - t, and d*
k - t, and d*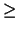 d. Thus
Theorem 3.6 implies
d. Thus
Theorem 3.6 implies
Now let
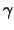 = c/n, and notice that
t/n
= c/n, and notice that
t/n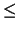
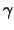 .
Hence if
.
Hence if
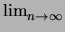
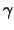 = 0, then (3.21)
asymptotically reduces to
d
= 0, then (3.21)
asymptotically reduces to
d 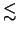 2/R, as in (3.1).
Thus to support an asymptotically good sequence of codes,
c must grow linearly with n, which means
that the number of cycles 2c grows exponentially
with n.
It would be useful to find out how
the parameter
2/R, as in (3.1).
Thus to support an asymptotically good sequence of codes,
c must grow linearly with n, which means
that the number of cycles 2c grows exponentially
with n.
It would be useful to find out how
the parameter
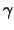 = c/n, which has to do with
the number of cycles, trades off versus the traditional
asymptotic parameters
= c/n, which has to do with
the number of cycles, trades off versus the traditional
asymptotic parameters
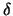 = d /n and R = k/n as
n
= d /n and R = k/n as
n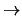
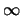 .
It would be also interesting to investigate, at least
asymptotically, codes that have Tanner graphs of prescribed
minimum girth.
.
It would be also interesting to investigate, at least
asymptotically, codes that have Tanner graphs of prescribed
minimum girth.
http://people.bu.edu/trachten