There is an interesting link between maximum likelihood decoding
and boolean formula satisfiability. Specifically, given a
noise-corrupted input z, the problem of maximum-likelihood decoding on a binary channel
is to find the vector c
closest in Hamming distance to z which satisfies the following parity-check equation over
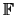 2:
2:
We can translate Equation (4.1) into a satisfiability problem by associating
each row in H with a clause of XOR'ed literals. Thus a row
[1, 0, 0, 1, 0, 0, 1] might
correspond to
c1 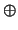 c4
c4 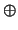 c7, where ci refers to the value of the i-th input
symbol and
c7, where ci refers to the value of the i-th input
symbol and 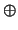 denotes XOR. Finding a maximum-likelihood decoding is thus akin to
finding the fewest bit flips of z needed to satisfy the conjunction of the negation of
these clauses.
This translation into the realm of boolean formulae opens the door to a vast
array of literature in computer science.
denotes XOR. Finding a maximum-likelihood decoding is thus akin to
finding the fewest bit flips of z needed to satisfy the conjunction of the negation of
these clauses.
This translation into the realm of boolean formulae opens the door to a vast
array of literature in computer science.
http://people.bu.edu/trachten