Next: Bibliography Up: Error-Correcting Codes on Graphs: Previous: Bounding decoding complexity Contents
We will show that each of the three relations (3.11),(3.13),(3.14) between n, k, and d derived in Section4.2 implies (3.9), providing d is an integer in (3.11),(3.13) and d is an odd integer in (3.14). In order to make the appendix self-contained, we now re-state these inequalities:
| d |
(9) |
d 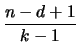 - 2 - 2 |
(11) |
| d |
(12) |
Notice that what we are trying to establish has nothing to do with graphs or codes; this is just manipulation of integer inequalities. In particular, we have following simple lemma.
Lemma11.
If
a ![]() b/c and a, b, c are positive integers,
then
a
b/c and a, b, c are positive integers,
then
a ![]() (b + a)/(c + 1).
(b + a)/(c + 1).
The proof of Lemma11 is straightforward, and is left to the reader. We first deal with (3.14), assuming d is odd. Taking the common denominator and applying (twice) Lemma11, we see that (3.14) implies
Since (d + 1)/2 is an integer for odd d, it follows from (20)
that
![]() .
This may be re-written as:
.
This may be re-written as:
If
n + 1 ![]() 0 mod (k + 1) then
0 mod (k + 1) then
![]() ,
and (21) clearly implies (3.9).
If
(n + 1)/(k + 1) is an integer, then
(21) is precisely the
equivalent form of (3.9) given in (3.12).
,
and (21) clearly implies (3.9).
If
(n + 1)/(k + 1) is an integer, then
(21) is precisely the
equivalent form of (3.9) given in (3.12).
It is easy to see that if d is an odd integer,
then (3.11) implies (3.14). Since this case
was already established above, it remains
to prove (3.11) for even d. Using once again
Lemma11, we see that (3.11) implies
d![]() 2n/(k + 1),
or equivalently
d /2
2n/(k + 1),
or equivalently
d /2![]() n/(k + 1). Since d /2 is
an integer for even d, we can take the integer part
of n/(k + 1) in the above expression. It follows that for even d, we have
n/(k + 1). Since d /2 is
an integer for even d, we can take the integer part
of n/(k + 1) in the above expression. It follows that for even d, we have
http://people.bu.edu/trachten