Tanner graphs

A Tanner graph for a binary (n, k, d ) code $\ensuremath{\mathbb{C}}$ is a bipartite graph whose adjacency matrix is the parity-check matrix of $\ensuremath{\mathbb{C}}$. The left part of the graph consists of site nodes which correspond to symbol bits of the code, and the right part of the graph consists of check nodes which correspond to parity checks in the graph. Thus the number of edges in any Tanner graph for a linear code  $\mathbb {C}$ of length n is O(n²), so that the graph's complexity grows quadratically with length, regardless of the code. Figure 1.5 gives a parity-check matrix and corresponding Tanner graph for a sample binary, linear code.

Figure 1.5: H is the parity-check matrix for a (5, 2, 3) binary, linear code. The accompanying figure is its Tanner graph, in which the left nodes correspond to symbol bits and the right nodes correspond to parity-checks.

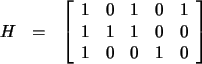A generalized version of the Viterbi algorithm, known as the min-sum algorithm [66], might allow for decoding with Tanner graphs. This is an iterative algorithm which tries to spread bit-error information throughout the Tanner graph. Thus, check nodes repeatedly minimize error among legal site configurations neighboring them, and site nodes repeatedly sum errors from their neighbors. This iterative algorithm provenly converges [1,55,66] to a maximum-likelihood decision for cycle-free Tanner graphs, although it does not necessarily converge or decode correctly if the graph has a cycle. Thus, if we can represent $\ensuremath{\mathbb{C}}$ by a Tanner graph without cycles, then maximum-likelihood decoding of $\ensuremath{\mathbb{C}}$ can be achieved in time O(n²) using the min-sum algorithm.