Bounding Length

By summing Theorem 4 over many iterations, we may obtain a lower bound on the length n_m of the m-th code of any minimal $\ensuremath{{\mathfrak{G}}}$ -family.

Corollary 2 For any trivially seeded, minimal $\ensuremath{{\mathfrak{G}}}$ -code,

n_m $\displaystyle \leq$ $\displaystyle \left(\vphantom{m+\frac{1}{2}}\right.$ m + $\displaystyle {\textstyle\frac{1}{2}}$ $\displaystyle \left.\vphantom{m+\frac{1}{2}}\right)$ $\displaystyle {\frac{d+4}{3}}$ - $\displaystyle {\textstyle\frac{2}{3}}$ .

Proof: Consider summing a weaker inequality obtained from Theorem 4 by eliminating the floor function. Summing over iterations 1...m of the $\mathfrak{G}$ -construction we get:

$\displaystyle \sum_{i=1}^{m}$ $\displaystyle \rho_{i}^{}$	$\displaystyle \geq$	$\displaystyle \sum_{i=1}^{m}$ $\displaystyle \left(\vphantom{{d - \frac{\rho_{i-1}}{2} - 2}}\right.$ d- $\displaystyle {\frac{\rho_{i-1}}{2}}$ -2 $\displaystyle \left.\vphantom{{d - \frac{\rho_{i-1}}{2} - 2}}\right)$
	$\displaystyle \geq$	m(d - 2) - $\displaystyle {\textstyle\frac{1}{2}}$ $\displaystyle \sum_{i=0}^{{m}-1}$ $\displaystyle \rho_{i}^{}$ .

Noting that for trivially seeded codes, $\rho_0 = \ensuremath {\left\lfloor \frac{d}{2} \right\rfloor}$ and $\rho_{m}^{}$ $\geq$ 0, we may reduce this to:

$\displaystyle {\textstyle\frac{3}{2}}$ $\displaystyle \sum_{i=1}^{{m}}$ $\displaystyle \rho_{i}^{}$ $\displaystyle \geq$ I>m(d - 2) - $\displaystyle {\textstyle\frac{1}{2}}$ ( $\displaystyle \rho_{0}^{}$ - $\displaystyle \rho_{m}^{}$ ) $\displaystyle \geq$ I>m(d - 2) - $\displaystyle {\frac{d}{4}}$ .

Furthermore, since we are dealing with minimal $\ensuremath{{\mathfrak{G}}}$ -codes,

n_m = tex2html_image_mark>#tex2html_wrap_indisplay7503# $\displaystyle \left(\vphantom{ d-\rho_i }\right.$ d - $\displaystyle \rho_{i}^{}$ $\displaystyle \left.\vphantom{ d-\rho_i }\right)$ = I>md - $\displaystyle \sum_{i=1}^{m}$ $\displaystyle \rho_{i}^{}$

so that we may now conclude the proof:

n_m	= md - $\displaystyle \sum_{i=1}^{m}$ $\displaystyle \rho_{i}^{}$
	$\displaystyle \leq$ md - $\displaystyle {\textstyle\frac{2}{3}}$ $\displaystyle \left(\vphantom{ {m}(d-2) - \frac{d}{4}}\right.$ m(d - 2) - $\displaystyle {\frac{d}{4}}$ $\displaystyle \left.\vphantom{ {m}(d-2) - \frac{d}{4}}\right)$
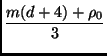	$\displaystyle \leq$ $\displaystyle {\frac{m}{3}}$ (d + 4) + $\displaystyle {\frac{d}{6}}$ .

width4pt depth2pt height6pt

In the case of a $\ensuremath{{\mathfrak{G}}}$ -family seeded by a non-trivial code of length n₀ and covering radius $\rho_{0}^{}$ , Corollary 2 may be easily generalized to

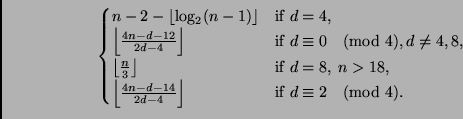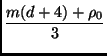n_m $\displaystyle \leq$ n₀ + $\displaystyle {\frac{m(d+4)+\rho_0}{3}}$ + $\displaystyle {\frac{d}{6}}$ .

Clearly, Corollary 2 applies to all lexicodes and trellis-oriented lexicodes. It is a asymptotically tighter than the similar bound given by Brualdi and Pless [3, Theorem3.5]:

k $\displaystyle \geq$ $\begin{displaymath}\begin{cases} n-2-\ensuremath {\left\lfloor \log_2(n-1) \rig... ...d-4} \right\rfloor}&\text{if } d \equiv 2 \pmod{4}. \end{cases}\end{displaymath}$

(12)

Specifically, Corollary 2 asymptotically binds k $\geq$ 3 ${\frac{n}{d}}$ whereas Equation (15) binds k $\geq$ 2 ${\frac{n}{d}}$ . Nevertheless, both of these bounds are weak as illustrated by Appendix .1.