Next: The structure of cycle-free Up: Tanner-Graph Decoding Previous: History Contents
Let
H = [hij] be an
r×n matrix, with entries drawn from
the finite field
IFq of order q. We let * denote a nonzero entry
in H. Given H, we define a bipartite graph T as follows: the
vertex set of T consists of the set
![]() = {x1, x2,..., xn}
of symbol vertices and the set
= {x1, x2,..., xn}
of symbol vertices and the set
![]() = {y1, y2,..., yr} of
check vertices;
there is an edge (yi, xj) in T if and only if
hij = *.
Thus the neighborhood of the vertex
yi
= {y1, y2,..., yr} of
check vertices;
there is an edge (yi, xj) in T if and only if
hij = *.
Thus the neighborhood of the vertex
yi![]()
![]() corresponds to the i-th
row of H, and the neighborhood of the vertex
xj
corresponds to the i-th
row of H, and the neighborhood of the vertex
xj![]()
![]() corresponds
to the j-th column of H. We say that T is the Tanner graph of
H, and denote T = T(H). It is obvious that every matrix defines a unique
Tanner graph. Over
IF2, the converse is also true: every bipartite
graph T defines a unique binary matrix H such that T = T(H), which
is the
corresponds
to the j-th column of H. We say that T is the Tanner graph of
H, and denote T = T(H). It is obvious that every matrix defines a unique
Tanner graph. Over
IF2, the converse is also true: every bipartite
graph T defines a unique binary matrix H such that T = T(H), which
is the
![]() ,
,![]() adjacency matrix of T.
adjacency matrix of T.
We say that a bipartite graph T represents the linear
code
![]() , or simply that T is a Tanner graph for
, or simply that T is a Tanner graph for
![]() , if
there exists a parity-check matrix H for
, if
there exists a parity-check matrix H for
![]() such that T
is the Tanner graph of H. In general, a given linear code
can be represented by many distinct Tanner graphs. On the
other hand, over
IF2, a given Tanner graph represents a unique
binary code.
such that T
is the Tanner graph of H. In general, a given linear code
can be represented by many distinct Tanner graphs. On the
other hand, over
IF2, a given Tanner graph represents a unique
binary code.
We say that a matrix H is cycle-free if the corresponding Tanner
graph T(H) is cycle-free. Notice that every submatrix of a cycle-free
matrix is also cycle-free. We say that a linear code
![]() over
IFq is
cycle-free if there exists a cycle-free parity-check
matrix for
over
IFq is
cycle-free if there exists a cycle-free parity-check
matrix for
![]() . Observe that if the matrices H and H' differ
by a permutation of rows and columns then the
Tanner graphs T(H) and
T(H') are isomorphic. On the other hand, if H and H' differ by a sequence
of elementary row operations then T(H) and T(H') are generally not
isomorphic. Thus it is possible to have two parity-check matrices
for the same code, one of which is cycle-free while the other is not.
It is also possible to have two cycle-free Tanner graphs for the same
code that are not isomorphic.
. Observe that if the matrices H and H' differ
by a permutation of rows and columns then the
Tanner graphs T(H) and
T(H') are isomorphic. On the other hand, if H and H' differ by a sequence
of elementary row operations then T(H) and T(H') are generally not
isomorphic. Thus it is possible to have two parity-check matrices
for the same code, one of which is cycle-free while the other is not.
It is also possible to have two cycle-free Tanner graphs for the same
code that are not isomorphic.
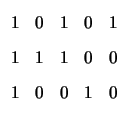
However, the code
![]() is, in fact, cycle-free
since adding the first row of H to the second row produces a cycle-free
parity-check matrix H' for
is, in fact, cycle-free
since adding the first row of H to the second row produces a cycle-free
parity-check matrix H' for
![]() .
The graph T(H') shown in Figure 3.1b is a cycle-free Tanner graph
for
.
The graph T(H') shown in Figure 3.1b is a cycle-free Tanner graph
for
![]() .
.
width4pt depth2pt height6pt
A cycle-free graph consisting of a single connected component is called a tree, and a multiple-component cycle-free graph will is a forest. The following simple lemma will serve as our starting point. This lemma is well-known in graph theory - see, for instance, West [64, p.52] - and is based on the fact that | E| = | V| - 1 for trees.
Since every forest contains at least one tree, we have
http://people.bu.edu/trachten