We now construct
a family of cycle-free codes that attain the bound of Theorem 3.6
with equality, for all values of n and k. The construction
is quite simple: as in Section 3.3,
we start with the single-parity-check code
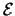 k+1 of dimension k,
and repeat the symbols of
k+1 of dimension k,
and repeat the symbols of
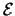 k+1 until a code
k+1 until a code
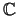 of length n
is obtained. It is obvious that the dimension of
of length n
is obtained. It is obvious that the dimension of
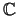 is k, and
by Lemma 3.4 this code is cycle-free. The minimum distance of
is k, and
by Lemma 3.4 this code is cycle-free. The minimum distance of
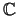 will depend on the sequence of symbol repetitions.
The idea is to
repeat each symbol in
will depend on the sequence of symbol repetitions.
The idea is to
repeat each symbol in
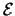 k+1 equally often and as much as possible.
For example, for n = 13 and k = 3, we obtain the following
parity-check matrix in reduced canonical form (0 bits have been
intentionally replaced with blank spaces to accentuate the structure
of the matrix):
k+1 equally often and as much as possible.
For example, for n = 13 and k = 3, we obtain the following
parity-check matrix in reduced canonical form (0 bits have been
intentionally replaced with blank spaces to accentuate the structure
of the matrix):
which defines a (13, 3, 6) cycle-free code.
In general, the number of symbols to be repeated is k + 1,
while the number of positions available is n - (k + 1).
Write:
n - (k + 1) = a(k + 1) + b
where a, b are integers, and
0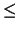 b
b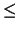 k. This
decomposition of the number of available positions
means that in our construction exactly k - b + 1 symbols
of
k. This
decomposition of the number of available positions
means that in our construction exactly k - b + 1 symbols
of
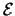 k+1 will be repeated
times, while the remaining b symbols of
k+1 will be repeated
times, while the remaining b symbols of
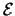 k+1
will be repeated a + 1 times. If b
k+1
will be repeated a + 1 times. If b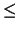 k - 1, then
at least two symbols of
k - 1, then
at least two symbols of
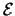 k+1 are repeated
exactly a times. Since
k+1 are repeated
exactly a times. Since
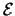 k+1 contains
a codeword of weight 2 in every two positions,
the minimum distance of the resulting code
k+1 contains
a codeword of weight 2 in every two positions,
the minimum distance of the resulting code
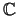 is
is
If b = k, then only one symbol in
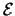 k+1
is repeated a times, while all the other
symbols are repeated a + 1 times. In this
case, the minimum distance of
k+1
is repeated a times, while all the other
symbols are repeated a + 1 times. In this
case, the minimum distance of
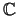 is
is
d = 2 + a + (a+1) = 2  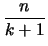  + 1 + 1 |
(9) |
Notice that b = k if and only if
n + 1  0 mod (k + 1).
Hence it follows from (3.17) and (3.18) that the
code
0 mod (k + 1).
Hence it follows from (3.17) and (3.18) that the
code
 constructed in this manner
attains the bound of Theorem 3.6 with equality.
constructed in this manner
attains the bound of Theorem 3.6 with equality.
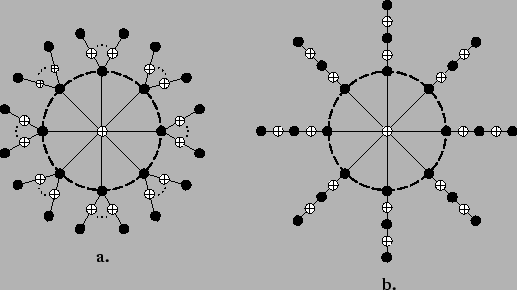
Figure 3.6 schematically shows two alternative cycle-free Tanner
graphs for codes resulting from this construction (compare the Tanner graph
in Figure 3.6a with Figure 3.2b).
Figure 3.6:
Two alternative Tanner graphs for optimal cycle-free codes.
 |
We point out that although cycle-free codes obtained by
repeating symbols in
 k+1 have the highest possible
minimum distance, they are not the only codes with this property. For example, consider the following
parity-check matrix in reduced canonical form:
k+1 have the highest possible
minimum distance, they are not the only codes with this property. For example, consider the following
parity-check matrix in reduced canonical form:
It is easy to see that this matrix defines a (13, 3, 6) cycle-free
code
 , whose distance attains the bound of Theorem 3.6 with equality.
This code was obtained by repeating symbols in a (5, 3, 2) code.
It can be readily verified that
, whose distance attains the bound of Theorem 3.6 with equality.
This code was obtained by repeating symbols in a (5, 3, 2) code.
It can be readily verified that
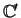 is not equivalent to
the (13, 3, 6) cycle-free code
is not equivalent to
the (13, 3, 6) cycle-free code
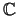 , defined by the parity-check
matrix in (3.16) and obtained by repeating symbols
in
, defined by the parity-check
matrix in (3.16) and obtained by repeating symbols
in
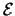 4. For instance,
4. For instance,
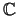 contains the all-one codeword,
while
contains the all-one codeword,
while
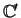 does not.
does not.
http://people.bu.edu/trachten
![]() k+1 have the highest possible
minimum distance, they are not the only codes with this property. For example, consider the following
parity-check matrix in reduced canonical form:
k+1 have the highest possible
minimum distance, they are not the only codes with this property. For example, consider the following
parity-check matrix in reduced canonical form: