Next: Trellis-oriented lexicodes Up: Instances of the G-construction Previous: Instances of the G-construction Contents
In order to compute
![]() we will first transform the generator
matrix of the code into a minimal span generator matrix (MSGM) form,
in which the sum of the spans of the generators is minimized.
Adapting the notation in [43], the span of a binary n-vector
x = (x1, x2, x3,..., xn) is
we will first transform the generator
matrix of the code into a minimal span generator matrix (MSGM) form,
in which the sum of the spans of the generators is minimized.
Adapting the notation in [43], the span of a binary n-vector
x = (x1, x2, x3,..., xn) is
![]() , where
, where
![]() and
and
![]() are the rightmost (i.e. largest) and leftmost (i.e.
smallest) index i, respectively, such that
xi
are the rightmost (i.e. largest) and leftmost (i.e.
smallest) index i, respectively, such that
xi ![]() 0. Thus,
the span of the vector
x = (0001001100) is
0. Thus,
the span of the vector
x = (0001001100) is
![]() . We
can efficiently transform any matrix into MSGM-form using the greedy
algorithm in [43]. We note that two vectors of an MSGM
cannot have their leftmost or their rightmost index in common, or else
they may be added to produce a generator matrix with shorter span.
. We
can efficiently transform any matrix into MSGM-form using the greedy
algorithm in [43]. We note that two vectors of an MSGM
cannot have their leftmost or their rightmost index in common, or else
they may be added to produce a generator matrix with shorter span.
Given an MSGM for a code and a set of coset representatives
![]() , Method 2.2 computes the lexicographically
earliest vector among the cosets represented in
, Method 2.2 computes the lexicographically
earliest vector among the cosets represented in
![]() .
.
1. for v = (v1, v2, v3,..., vn)do
2. fori from n downto 1
3. ifis a 1 then
4. vv + Gi
5. store the modified v;
6. among all stored v, return the lexicographically earliest
This method looks for the generators whose left-most 1-bit corresponds
to 1-bits in vectors
v![]() V.
Figure 2.4 demonstrates this method with
the set
V.
Figure 2.4 demonstrates this method with
the set
![]() = {1010000} on the (7, 4, 3) code described in
Figure 2.2. For this case, the vector 0001011 is the
lexicographically earliest vector in the same coset as 1110000.
Note that the ordering of the
generators in the MSGM is significant and that different orderings
might not yield the lexicographically earliest vector.
Thus, if generators G2 and G3 are switched, then Method 2.2
yields 0010010, which is
not the lexicographically earliest vector desired.
= {1010000} on the (7, 4, 3) code described in
Figure 2.2. For this case, the vector 0001011 is the
lexicographically earliest vector in the same coset as 1110000.
Note that the ordering of the
generators in the MSGM is significant and that different orderings
might not yield the lexicographically earliest vector.
Thus, if generators G2 and G3 are switched, then Method 2.2
yields 0010010, which is
not the lexicographically earliest vector desired.
|
We will now prove the correctness and complexity bounds of
Method 2.2. In our applications,
![]() will
typically be the set of coset leaders with maximum distance from
will
typically be the set of coset leaders with maximum distance from
![]() ,
in which case Method 2.2 computes precisely
,
in which case Method 2.2 computes precisely
![]() .
.
Proof of Method 2.2. We first show correctness of the
method by proving that, for each
v![]()
![]() , lines 2-5
compute the lexicographically earliest vector in the same coset as
v. This way, line 6 in the method will return the lexicographically
earliest vector among all the cosets represented.
, lines 2-5
compute the lexicographically earliest vector in the same coset as
v. This way, line 6 in the method will return the lexicographically
earliest vector among all the cosets represented.
We know from [43, Thm 6.11 and Lemma 6.7] that the rows of G have the predictable support property:
| span |
(9) |
Now suppose that vbest is the lexicographically earliest vector in the same coset as v, but that instead vstored is the vector stored on line 5 of the method. Our goal will be to show that the difference between these two vectors, denoted vdiff, is in fact 0.
Clearly v, vbest, and vstored are necessarily in the same
coset of
![]() . Moreover, since v and vstored are in the same coset, vdiff
must be a code word of
. Moreover, since v and vstored are in the same coset, vdiff
must be a code word of
![]() so that we can write (for an appropriate
set Jdiff):
so that we can write (for an appropriate
set Jdiff):
vdiff = 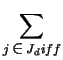 Gj Gj |
(9) |
Assume (for sake of contradiction) that L(vdiff )= k, meaning that the left-most 1 bit of vdiff occurs at the k-th index. This implies that, starting from the left-most bit, vbest and vstored are identical until the k-th index, on which they differ. Since, by definition, vbest comes lexicographically before vstored, it must be that vbest has a 0 and vstored a 1 at the k-th index. However, (2.5) then implies that there must be some generator vector Gj whose left-index is k, contradicting our constructive generation of vstored. Thus, the left-index of vdiff could not possibly be at location k, for any k, so that vdiff must be 0 and correctness of the method is proved.
The space bound for this method follows straightforwardly, as at any
point in the algorithm we need to actively store only the
lexicographically earliest vector among those determined on line 5 so
far. The time bound follows from the fact that lines 3-5 are each
computable in constant time, giving a running time of O(n| V|) for
lines 1-5; Line 6 can be computed with constant overhead on-line, as
each vector is stored.
width4pt depth2pt height6pt
Method 2.2 provides a fast way of computing the lexicographic generating mapping. Appendix A.1 gives computed parameters for many lexicodes that were thus computed. This list is more exhaustive than what is currently available in the literature [9,14].
http://people.bu.edu/trachten