Next: Bounds on code parameters Up: Lexicographic Codes Previous: Trellis-bounded lexicodes Contents
So far we have addressed the computation of various generating mappings. In this and subsequent sections we will complete our analysis by addressing the theoretical mechanism which supports the G-construction. Specifically, the G-construction establishes an important relationship between the coset leaders of the codes produced at successive iterations. This relationship allows us to efficiently compute the coset leaders of many G-codes (and hence their generator matrices) as well as to determine bounds on their code parameters. We describe this relationship by first associating a companion with each coset leader.
We show that one iteration of the lexicographic construction produces
a code whose coset leaders are the lower-weight vectors between
![]() a| u
a| u![]() and
and
![]()
![]() |
|![]() (u)
(u)![]() , for each vector a of appropriate
size and coset leader u in the original code. Here
, for each vector a of appropriate
size and coset leader u in the original code. Here ![]() refers to the complement of a.
refers to the complement of a.
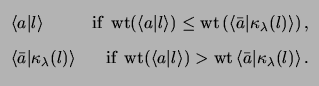
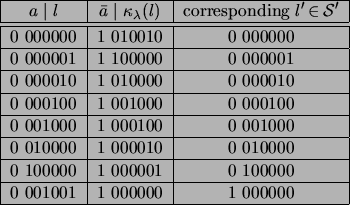
Figure 2.6 demonstrates the use of the ![]() correspondence to generate the coset leaders of the (7, 3, 4) binary
lexicode
correspondence to generate the coset leaders of the (7, 3, 4) binary
lexicode
![]() from the coset leaders of the (6, 2, 4) binary
lexicode
from the coset leaders of the (6, 2, 4) binary
lexicode
![]() over the base field
over the base field
![]() 2.
Specifically, in this example,
2.
Specifically, in this example,
![]() and
and
![]() The coset leaders of
The coset leaders of
![]() are
are
 |
Proof of Theorem 2.5. We introduce the following notation to simply the proof:
| g(a, l ) + h(a, l ) | = |
|
| = |
||
The second observation of this proof is that
g(a, l ) and
g(a', l') are generally not in the same coset of
![]() . More
specifically, these two vectors are in the same coset precisely when
l and l' are in distinct cosets of
. More
specifically, these two vectors are in the same coset precisely when
l and l' are in distinct cosets of
![]() and
and
![]()
![]() a'. To see this we analyze the two possibilities for the sum
g(a, l )+ g(a', l'). In the first case, its leading bits are
neither 0
a'. To see this we analyze the two possibilities for the sum
g(a, l )+ g(a', l'). In the first case, its leading bits are
neither 0![]() nor 1
nor 1![]() . Alternatively, its leading bits
are 0
. Alternatively, its leading bits
are 0![]() but its trailing bits are the sum of distinct coset
leaders
but its trailing bits are the sum of distinct coset
leaders
![]() . Both possibilities preclude
g(a, l )+ g(a', l') from being a codeword of
. Both possibilities preclude
g(a, l )+ g(a', l') from being a codeword of
![]() , proving
the observation.
, proving
the observation.
Based on the above two observations,
g( . , . ) and
h( . , . ) represent the same two-to-one correspondence
between (vector, coset-leader) pairs (a, l ) and the cosets of
![]() .
In fact, for each
a
.
In fact, for each
a![]()
![]() 2n and coset leader l of
2n and coset leader l of
![]() , the coset of
g(a, l ) contains only the vectors:
, the coset of
g(a, l ) contains only the vectors:
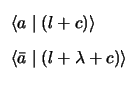
In addition, for any
![]() ,
g(a, l ) cannot have weight
greater than the weight of
,
g(a, l ) cannot have weight
greater than the weight of
![]() a|(l + c)
a|(l + c)![]() , because l is
a coset leader, and
h(a, l ) cannot have weight greater than
, because l is
a coset leader, and
h(a, l ) cannot have weight greater than
![]()
![]() |(l +
|(l + ![]() + c)
+ c)![]() . Thus, all the vectors in the
coset containing
g(a, l ) will have weight
. Thus, all the vectors in the
coset containing
g(a, l ) will have weight
![]() , so that either
g(a, l ) or
h(a, l ) must be a coset leader in
, so that either
g(a, l ) or
h(a, l ) must be a coset leader in
![]() . Since
g(a, l ) and
h(a, l ) are correspondences,
. Since
g(a, l ) and
h(a, l ) are correspondences,
![]() ' is
the complete set of coset leaders of
' is
the complete set of coset leaders of
![]() '.
'.
width4pt depth2pt height6pt