Computations

Theorem 2.5 can be directly translated into an algorithm that computes G-families. The algorithm simply computes the coset leaders of G-codes in the family, from which the remaining parameters may be easily deduced. This computation scheme has the advantage of being dependent on the co-dimension (i.e. the dimension of the dual code) rather than the dimension or the length alone. Thus, this algorithm is efficient for high-rate codes, and it is presented in Algorithm 2.12.

In Algorithm 2.12 we reuse our earlier notation that ${\Delta_i} = d - \ensuremath{\operatorname{wt}}(f(\ensuremath{ {\emph G}_{\,i-1}}))$. Note that we assume that the coset leaders of the seed code are known or trivially derivable, as is often the case. The correctness of the algorithm follows immediately from Theorem 2.5. Moreover, we can also compute the running time and space of this algorithm in terms of $\left\ulcorner\vphantom{ m }\right.$m$\left.\vphantom{ m }\right\urcorner$ $\mbox{$\stackrel{\rm def}{=}$}$ n_m - m, the co-dimension of the m-th G-code,

Lemma 2..12   Using an oracle for computing the generating mapping, Algorithm 2.12 runs in space O(2^{$\left\ulcorner\vphantom{ m }\right.$m$\left.\vphantom{ m }\right\urcorner$}) and time O(n_m$\left\ulcorner\vphantom{ m }\right.$m$\left.\vphantom{ m }\right\urcorner$2^{$\left\ulcorner\vphantom{ m }\right.$m$\left.\vphantom{ m }\right\urcorner$}).

An oracle is simply a black box that computes a given function in constant time. In this case, we assume the existence of an oracle for computing the generating mapping because the complexity of such a computation can vary greatly among mappings. The proof of Lemma 2.13 follows from a straightforward analysis of the pseudo-code for Algorithm 2.12.

Proof.  At each iteration, Algorithm 2.12 stores the coset leaders of the code $\ensuremath{ {\emph G}_{\,i}}$ which it is computing and the companion of each leader. Thus, the algorithm requires space

$$% latex2html id marker 4515O(\ensuremath{\char93 \mbox{\te... ...m}}) = O(2^{n_m-m}) = O(2^{\left\ulcorner m \right\urcorner })$$

where $\left\ulcorner\vphantom{ m }\right.$m$\left.\vphantom{ m }\right\urcorner$ = n_m - m denotes the co-dimension and $\ensuremath{\char93 \mbox{\texttt{COSET}}_{m}}$ denotes the number of cosets of $\ensuremath{ {\emph G}_{\,m}}$.

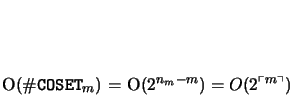
The time bound for this algorithm, on the other hand, is somewhat more complicated. Consider the innermost loop of the algorithm during the computation of the i-th extension. Clearly, based on Theorem 2.5, lines 6-10 are executed at most once for each coset of $\ensuremath{ {\emph G}_{\,i}}$. Moreover, the companion calculation in line 5 is executed once for each coset of $\ensuremath{ {\emph G}_{\,i-1}}$. The companion may be determined with a binary search over coset syndromes; the binary search requires time:

$$% latex2html id marker 4516O \left( log(\ensuremath{\char9... ...{COSET}}_{i-1}}) \right) = \left\ulcorner i-1 \right\urcorner$$

Finally, each syndrome calculation used to determine the companion of a coset of $\ensuremath{ {\emph G}_{\,i-1}}$ itself requires time O(n_i $\left\ulcorner\vphantom{ i }\right.$i$\left.\vphantom{ i }\right\urcorner$), corresponding to matrix-vector multiplications. Recall that our oracle supplies the computation in line 2 of this analysis in constant time.

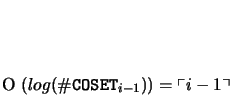
Putting everything together, we get a running time of

$$\left\ulcorner\vphantom{ i }\right. \left.\vphantom{ i }\right\urcorner \left[\vphantom{\, \left\ulcorner i-1 \right\urcorner +n_i(\left\ulcorner i \right\urcorner ) }\right. \left\ulcorner\vphantom{ i-1 }\right. \left.\vphantom{ i-1 }\right\urcorner \left\ulcorner\vphantom{ i }\right. \left.\vphantom{ i }\right\urcorner \left.\vphantom{\, \left\ulcorner i-1 \right\urcorner +n_i(\left\ulcorner i \right\urcorner ) }\right] \subset \left(\vphantom{2^{\left\ulcorner i \right\urcorner } \left\ulcorner i \right\urcorner n_i }\right. \left\ulcorner\vphantom{ i }\right. \left.\vphantom{ i }\right\urcorner \left\ulcorner\vphantom{ i }\right. \left.\vphantom{ i }\right\urcorner \left.\vphantom{2^{\left\ulcorner i \right\urcorner } \left\ulcorner i \right\urcorner n_i }\right)$$

Except for trivial cases, $\left\ulcorner\vphantom{ i }\right.$i$\left.\vphantom{ i }\right\urcorner$ and n_i do not decrease with i so that:

$$\sum_{{i=1}}^{{m}} \left\ulcorner\vphantom{ i }\right. \left.\vphantom{ i }\right\urcorner \left\ulcorner\vphantom{ i }\right. \left.\vphantom{ i }\right\urcorner \subseteq \left\ulcorner\vphantom{ m }\right. \left.\vphantom{ m }\right\urcorner \sum_{{i=1}}^{{m}} \left\ulcorner\vphantom{ i }\right. \left.\vphantom{ i }\right\urcorner$$

$$\subseteq \left\ulcorner\vphantom{ m }\right. \left.\vphantom{ m }\right\urcorner \left\ulcorner\vphantom{ m }\right. \left.\vphantom{ m }\right\urcorner$$

This proves the lemma.

width4pt depth2pt height6pt

For the specific case of distance 4 lexicodes, this algorithm is particularly fast, since Brualdi and Pless [9, Thm.3.5] show that, under these circumstances:

$$\left\lfloor\vphantom{ \log_2 (n_m-1) }\right. \left.\vphantom{ \log_2 (n_m-1) }\right\rfloor$$ (9)

so that Lemma 2.14 reduces to time O(n_m²log(n_m)) and space O(n_m). This is not surprising given that the distance 4 lexicodes are simply shortenings of the extended Hamming codes [14].

The analysis of Algorithm 2.12 assumes an oracle computation of the generating mapping. For the case of lexicodes and trellis-oriented lexicodes, however, Method 2.2 provides an efficient means of computing this mapping in time $O(n_m \times \ensuremath{\char93 \mbox{\texttt{COSET}}_{m}})$ and constant space. As in the case of lexicodes and trellis-oriented codes, the overhead of computing $f(\ensuremath{ {\emph G}_{\,i-1}})$ is usually eclipsed by the running time of the remainder of the algorithm.

Corollary 2..13   Algorithm 2.12 requires time O(n_m$\left\ulcorner\vphantom{ m }\right.$m$\left.\vphantom{ m }\right\urcorner$2^{$\left\ulcorner\vphantom{ m }\right.$m$\left.\vphantom{ m }\right\urcorner$}) and space O(2^{$\left\ulcorner\vphantom{ m }\right.$m$\left.\vphantom{ m }\right\urcorner$}) to compute lexicodes and trellis-oriented lexicodes.

The complexity of Algorithm 2.12 is thus bounded by the co-dimension of the code and by the difficulty of computing the generating mapping. Under practical conditions, we were able to compute lexicodes well beyond length 44 initially reported in [14].

In addition, we were able to construct trellis-oriented codes with code parameters rivaling those of lexicodes, but with much better trellis state complexities. As an example, we generated trellis-oriented G-code with code parameters similar to lexicodes, but with better state complexity than the corresponding BCH codes heuristically minimized in [34]. These result were predicted by [34] and are demonstrated n Figures 2.7 and 2.8.

Figure 2.7: A comparison of the state complexities of the (32, 16, 8) trellis-oriented lexicode (trelli) and the (32, 16, 8) extended BCH code (ext BCH) heuristically minimized in [34]

Figure 2.8: A comparison of the state complexities of the (31, 16, 7) trellis-oriented lexicode (Trelli) and a (31, 16, 7) extended BCH code (BCH) heuristically minimized in [34]

Finally, the trellis state bounded codes that we have computed show improvements, for various code parameters, over the similar codes computed in [67] using different techniques.Figure 2.9 depicts the generator matrix of the (70, 49, 8) trellis-oriented code produced using Algorithm 2.12. Other examples and computations of the various techniques described in this paper are available in Appendix A.

Figure: The (70, 49, 8) trellis-oriented G-code.