



Next: System Model
Up: PDA Synchronization
Previous: Results
Contents
Probabilistic CPISync
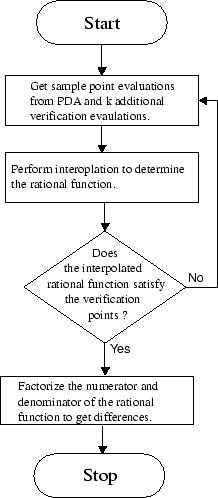
Figure 3.8:
Probabilistic
scheme
 |
An extension of CPISync when the upper bound on the number of
differences between the reconciling hosts is not know is performed
in the following manner.
In general, the two hosts keep guessing
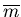 until the
resulting polynomials agree in all
until the
resulting polynomials agree in all 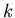 sample points. A precise
probabilistic analysis in [14] shows that such an
agreement corresponds to a probability of error
sample points. A precise
probabilistic analysis in [14] shows that such an
agreement corresponds to a probability of error
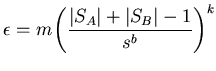 |
(3.3) |
where 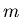 is the number of differences between the two reconciling
hosts
is the number of differences between the two reconciling
hosts 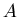 and
and 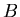 .
Using a trivial upper bound
.
Using a trivial upper bound
 we see
that an arrangement of
we see
that an arrangement of
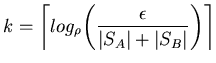 |
(3.4) |
samples (where
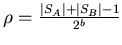 ) to get a
probability of error
) to get a
probability of error 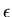 for the whole protocol. Thus, for
example reconciling host sets of
for the whole protocol. Thus, for
example reconciling host sets of 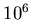 ,
, 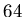 -bit integers with
error probability
-bit integers with
error probability
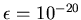 would require agreement of
would require agreement of
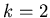 random samples.
This verification protocol requires the transmission of at most
random samples.
This verification protocol requires the transmission of at most 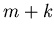 samples and one random number seed (for generating random
sample points) to reconcile two sets; the value
samples and one random number seed (for generating random
sample points) to reconcile two sets; the value 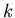 is determined
by the desired probability of error
is determined
by the desired probability of error 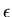 using the above
expression for
using the above
expression for 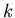 . The
. The 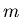 sample points are used to interpolate
a rational function, corresponding to a guess of the differences
between the two machines, and the latter
sample points are used to interpolate
a rational function, corresponding to a guess of the differences
between the two machines, and the latter 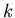 points are used to
verify the correctness of this guess. If the verification
succeeds, the synchronization is complete. On the other hand, if
verification fails, then the PC collects all the sample points
seen so far into a guess of the differences between the two
machines at the same time requesting
points are used to
verify the correctness of this guess. If the verification
succeeds, the synchronization is complete. On the other hand, if
verification fails, then the PC collects all the sample points
seen so far into a guess of the differences between the two
machines at the same time requesting 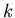 additional random
evaluations from the PDA to confirm its new guess. This procedure
is iterated until the verification succeeds, at which point the
synchronization is complete. Since
additional random
evaluations from the PDA to confirm its new guess. This procedure
is iterated until the verification succeeds, at which point the
synchronization is complete. Since 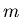 evaluations will
necessarily be enough to completely determine up to
evaluations will
necessarily be enough to completely determine up to 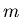 differences, verifications will necessarily succeed after at most
differences, verifications will necessarily succeed after at most
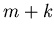 transmissions. Figure 3.8 shows a
flowchart of probabilistic CPISync.
Thus, though the verification protocol will require more rounds of
communication for synchronization that the Deterministic CPISync,
it will not require transmission of significantly more bits of
information. We see in the next section that the computational
overhead of this protocol is also not large.
transmissions. Figure 3.8 shows a
flowchart of probabilistic CPISync.
Thus, though the verification protocol will require more rounds of
communication for synchronization that the Deterministic CPISync,
it will not require transmission of significantly more bits of
information. We see in the next section that the computational
overhead of this protocol is also not large.
Subsections




Next: System Model
Up: PDA Synchronization
Previous: Results
Contents
Sachin Kumar Agarwal
2002-07-12
