



Next: Results
Up: Probabilistic CPISync
Previous: Probabilistic CPISync
Contents
From an end-user perspective, the most important metric of
usability of any synchronization protocol is the latency in the
synchronization process. We therefore consider optimizing the
latency with the view of minimizing it. We thus propose a scheme
whose completion time is at worst a constant 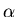 times larger
than the time needed to synchronize the two hosts when the number
of differences is know a priori (using the Deterministic scheme
discussed in 3.2 on page
times larger
than the time needed to synchronize the two hosts when the number
of differences is know a priori (using the Deterministic scheme
discussed in 3.2 on page ![[*]](file:/usr/share/latex2html/icons/crossref.png) ).
This probabilistic scheme retains one of the essential properties
of its deterministic counterpart: the synchronization latency
depends only on the number of differences and not on the total
size of the host data sets. We prove that
).
This probabilistic scheme retains one of the essential properties
of its deterministic counterpart: the synchronization latency
depends only on the number of differences and not on the total
size of the host data sets. We prove that
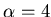 is the
optimal bound for this scheme and show how to achieve it.
is the
optimal bound for this scheme and show how to achieve it.
Figure 3.9:
A model of the approach
used to optimize the latency of synchronization when no bound is
known on the number of differences between data
sets.
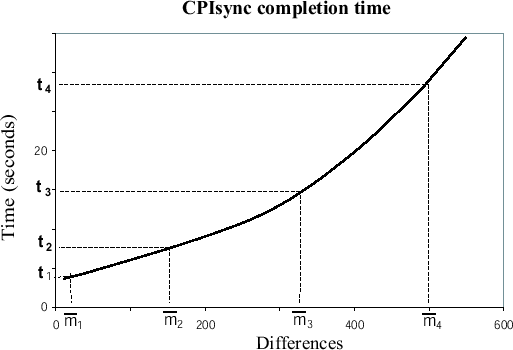 |
Our approach to this optimization relies in part on the data
graphed in Figure 2.7. We fit our data to a
polynomial regression that interpolates the latency of CPISync as
a function of the number of differences 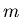 between the two hosts
as was shown in Table3.2. Since an exact value for
between the two hosts
as was shown in Table3.2. Since an exact value for
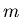 is not known at the start, the PDA and PC start with an
initial guess
is not known at the start, the PDA and PC start with an
initial guess
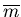 for an upper bound on
for an upper bound on 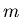 . In
Figure 3.9, this initial guess corresponds to a value
. In
Figure 3.9, this initial guess corresponds to a value
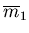 , which corresponds to a verification time of
, which corresponds to a verification time of
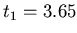 seconds. If verification fails this guess, we update our
bound to the value
seconds. If verification fails this guess, we update our
bound to the value
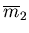 that corresponds to a
verification time that is
that corresponds to a
verification time that is 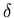 times larger than for
times larger than for
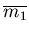 differences(i.e.
differences(i.e.
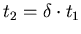 ). In the case of Figure 3.9,
). In the case of Figure 3.9,
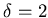 giving
giving
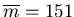 and
and
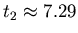 seconds. At each
iteration we guess the bound
seconds. At each
iteration we guess the bound
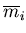 such that
such that
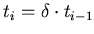 . We continue until verification succeeds for
some guessed bound
. We continue until verification succeeds for
some guessed bound
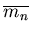 requiring time
requiring time
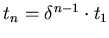 [13]:
Theorem 1 The latency-optimizing probabilistic
scheme takes at most
[13]:
Theorem 1 The latency-optimizing probabilistic
scheme takes at most
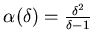 times longer than a deterministic scheme with an a priori
knowledge of the actual number of differences.
Proof: Denote by
times longer than a deterministic scheme with an a priori
knowledge of the actual number of differences.
Proof: Denote by 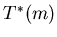 the synchronization latency
when
the synchronization latency
when 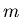 is know a priori, and by
is know a priori, and by 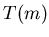 the synchronization
latency required by this probabilistic scheme. Furthermore, denote
by
the synchronization
latency required by this probabilistic scheme. Furthermore, denote
by 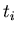 the time needed for the
the time needed for the 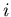 -th verification round in
which
-th verification round in
which
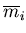 differences are guessed between the two
hosts.
Suppose that a correct upper bound,
differences are guessed between the two
hosts.
Suppose that a correct upper bound,
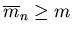 , is
observed first at the
, is
observed first at the 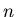 -th iteration, for
-th iteration, for 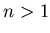 . The total
synchronization time required for the probabilistic scheme is then
simply the sum of the geometric progression
. The total
synchronization time required for the probabilistic scheme is then
simply the sum of the geometric progression
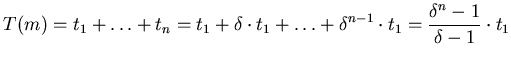 |
(3.5) |
Note that
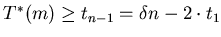 , since
, since
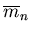 is assumed to be the first correct upper
bound
is assumed to be the first correct upper
bound 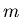 . We this obtain
. We this obtain
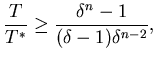 for all for all 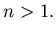 |
(3.6) |
It is easy to check that the right hand side of (3.6)
is maximized when
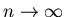 , meaning that
, meaning that
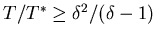 . By examining the derivative of
. By examining the derivative of
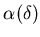 with respect to
with respect to 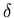 , one finds that this
function attains a minimum value at
, one finds that this
function attains a minimum value at 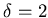 , leading to an
optimal ratio of
, leading to an
optimal ratio of 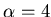 . Thus, the best policy for this scheme
is to double the verification time at each iteration.
. Thus, the best policy for this scheme
is to double the verification time at each iteration.
Figure 3.10:
A
comparison of the Probabilistic scheme with no known upper bound
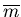 to the deterministic scheme with a given value of
to the deterministic scheme with a given value of
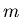 .
.
 |




Next: Results
Up: Probabilistic CPISync
Previous: Probabilistic CPISync
Contents
Sachin Kumar Agarwal
2002-07-12


